Segmentação por IA
Segmentação Automática de Lâminas Delgadas
A segmentação de imagens de lâminas petrográficas pode ser feita de duas formas: uma segmentação binária, que identifica apenas a fase de poro, e uma segmentação multifásica, que identifica os diversos minerais que compõem a rocha.
Segmentação Multifásica (Minerais)
A análise da composição mineral e da textura das rochas é fundamental para a indústria de petróleo. O GeoSlicer utiliza modelos de Deep Learning para automatizar essa análise a partir de imagens de lâminas, oferecendo uma alternativa ao método QEMSCAN.
Rede Neural Convolucional (U-Net)
Para a segmentação mineralógica, o GeoSlicer emprega uma rede neural convolucional com a arquitetura U-Net. Este tipo de rede é ideal para segmentação semântica, pois atribui uma classe a cada pixel da imagem, delimitando com precisão a região de cada elemento. A U-Net é composta por um caminho de codificação, que extrai características da imagem em múltiplas escalas, e um caminho de decodificação, que reconstrói o mapa de segmentação.
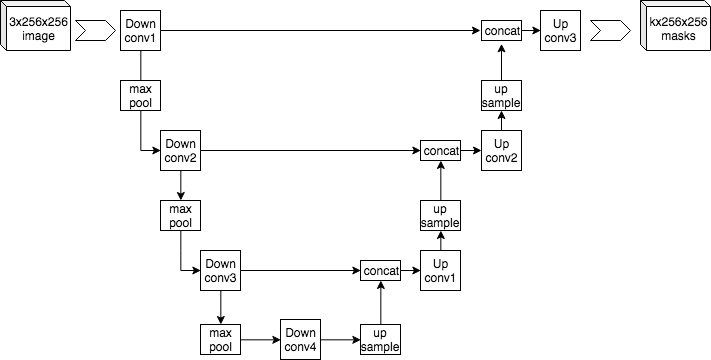 |
|---|
| Figura 1: Arquitetura exemplo da U-Net. |
Treinamento
O treinamento dos modelos foi realizado com mais de 50 lâminas de alta resolução, utilizando imagens de Luz Natural (PP) e Polarização Cruzada (PX). O resultado do QEMSCAN foi usado como gabarito. As imagens PP, PX e QEMSCAN foram alinhadas através de um processo de registro, e o treinamento focou em uma região de interesse (SOI) para minimizar ruídos de borda. Para aumentar a diversidade dos dados, os recortes das lâminas passaram por transformações aleatórias, como rotações e inversões. Os modelos foram treinados para identificar Poros e os minerais Calcita, Dolomita, Mg-Argilominerais, Quartzo e uma classe genérica de Outros.
Resultados
Os modelos finais, integrados ao GeoSlicer, apresentam boas aproximações da composição mineral, especialmente para o estudo de texturas e da distribuição das fases. Abaixo, um exemplo de predição sobre lâminas não vistas durante o treinamento.
 |
|---|
| Figura 2: Predição dos modelos finais sobre lâminas desconhecidas. |
Segmentação Poro/Não-poro
A porosidade é um indicador crucial do potencial de um reservatório. O GeoSlicer oferece métodos automáticos para segmentar os poros, que são tipicamente preenchidos com resina azul para destaque.
Redes Neurais Convolucionais (U-Net)
Assim como na segmentação multifásica, a arquitetura U-Net é utilizada para a segmentação de poros.
Treinamento
O modelo foi treinado com 85 imagens de lâminas, onde a segmentação de referência foi obtida por limiar de cor sobre a resina azul. As lâminas foram divididas em recortes de 128x128 pixels, e apenas as áreas úteis (delimitadas pela SOI) foram consideradas. O treinamento durou 300 épocas, com aplicação de modificações aleatórias (rotações, inversões) para diversificar os dados e melhorar a capacidade de generalização do modelo.
Resultados
O modelo alcançou um desempenho satisfatório, com um coeficiente de Dice (sobreposição) superior a 85%. Os resultados mostram que a rede consegue identificar os poros com alta confiança, embora possa apresentar algumas dificuldades nas bordas, onde as cores são intermediárias.
  |
|---|
| Figura 3: Exemplos de resultados. Em verde, os verdadeiros positivos; em vermelho, os falsos positivos; e em amarelo, os falsos negativos. |
Inferência Bayesiana
Como alternativa às redes neurais, a Inferência Bayesiana oferece um modelo mais simples para a segmentação poro/não-poro. Este método utiliza a regra de Bayes para calcular a probabilidade de um pixel pertencer a um segmento (poro ou não-poro) com base em uma média e uma matriz de covariância aprendidas durante o treinamento.
A abordagem utiliza uma Distribuição Normal Multivariada como função de verossimilhança:
Onde \(x_p\) é o vetor de pixels em uma janela, e \(\mu_s\) e \(\Sigma_s\) são a média e a covariância do segmento \(s\).
Treinamento e Resultados
Para melhorar os resultados, as imagens de lâmina, originalmente em formato RGB, são convertidas para HSV. O modelo foi treinado em um conjunto de dados pequeno (~10 amostras) e, mesmo com uma abordagem simples, produz resultados interessantes para a segmentação poro/não-poro.
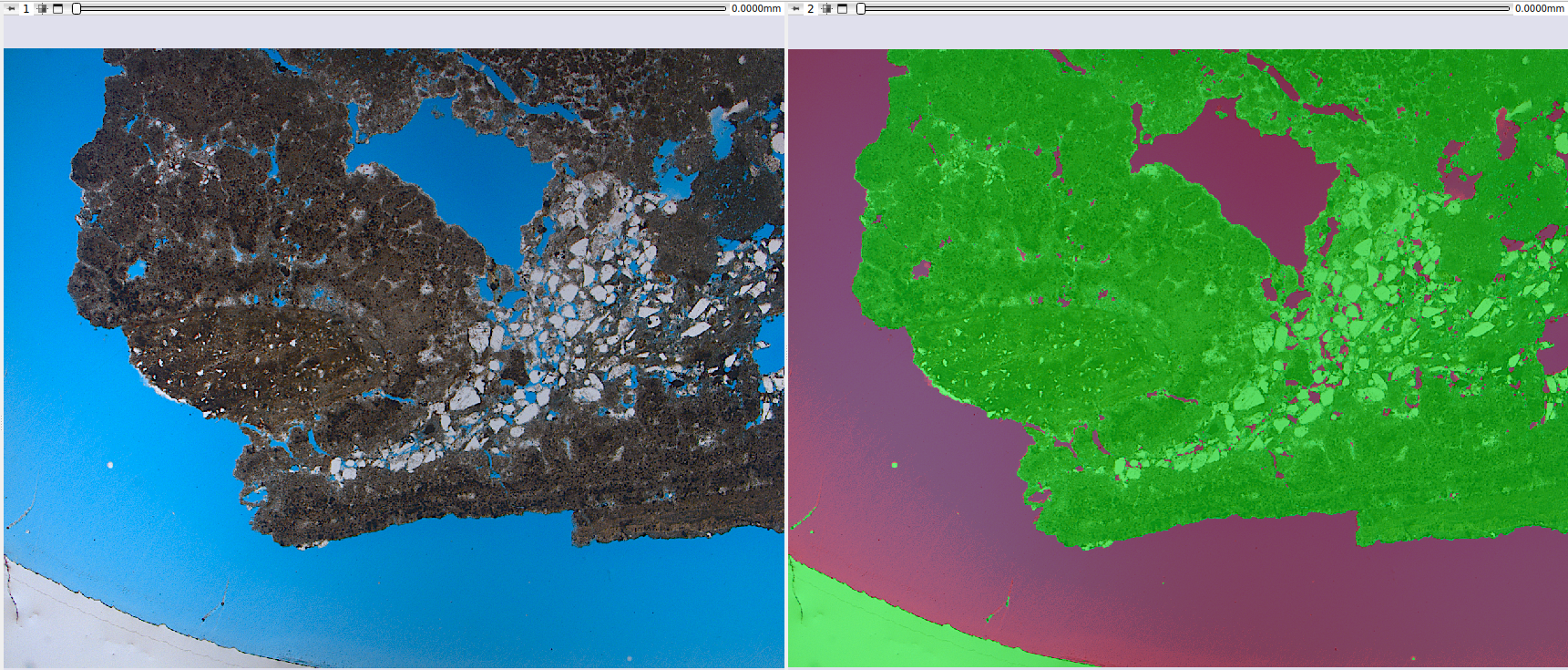 |
|---|
| Figura 4: Resultado qualitativo da segmentação poro/não-poro por inferência Bayesiana. |
Referências
-
DE FIGUEIREDO, L. P. et al. (2020). Direct Multivariate Simulation - A stepwise conditional transformation for multivariate geostatistical simulation. Computers & Geosciences.
-
DE FIGUEIREDO, L. P. et al. (2017). Bayesian seismic inversion based on rock-physics prior modeling for the joint estimation of acoustic impedance, porosity and lithofacies. Journal of Computational Physics.
-
HUNT, B. R. (1977). Bayesian methods in nonlinear digital image restoration. IEEE Transactions on Computers.
-
SKILLING, J. & BRYAN, R. K. (1984). Maximum entropy image reconstruction: general algorithm. Monthly Notices of the Royal Astronomical Society.
-
HANSON, K. (1993). Introduction to Bayesian image analysis. Proc SPIE.
-
HANSON, K. (1990). Object detection and amplitude estimation based on maximum a-posteriori reconstructions. Proc. SPIE.
-
GEMAN, S. & GEMAN, D. (1990). Stochastic Relaxation, Gibbs Distribution and the Bayesian Restoration of Images. IEEE, Transactions on Pattern Analysis; Machine Intelligence.
-
AITKIN, M. A. (2010). Statistical inference: an integrated Bayesian/likelihood approach. CRC Press.
-
MIGON, H. S. et al. (2014). Statistical Inference: An Integrated Approach. 2nd ed. CRC Press.
-
GAMERMAN, D. & LOPES, H. F. (2006). Monte Carlo Markov Chain: Stochastic Simulation for Bayesian Inference. 2nd ed. Chapman & Hall.