Segmentação por IA
Treinamento de Modelo
O módulo MicroCT Segmenter oferece a opção de Model Training, que realiza a segmentação de uma amostra inteira a partir de uma anotação inicial simples. Com base nessa anotação, diferentes métodos treinam um modelo e inferem o resultado em toda a imagem ou em uma região de interesse (SOI). O modelo treinado pode ser salvo e reutilizado em outras imagens.
Método Random-Forest
O Random-Forest é um método que constrói múltiplas árvores de decisão durante o treinamento para criar um modelo robusto. A classificação final é determinada pela maioria dos votos das árvores. Para este método, é possível selecionar diferentes features (características) extraídas da imagem para o treinamento.
Seleção de características (features)
- Raw input image: Adiciona a própria imagem como uma das entradas.
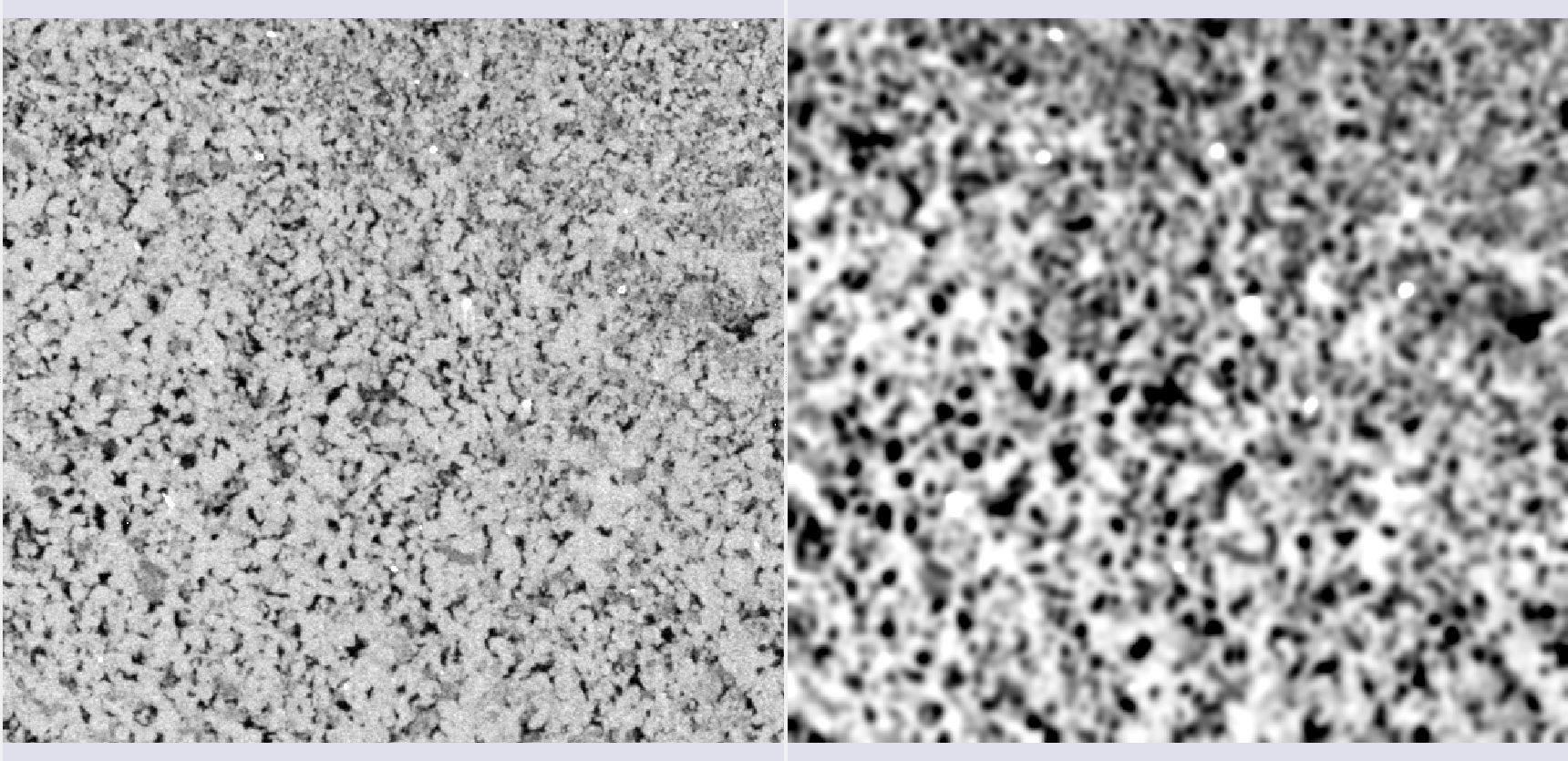
- Gaussian filter: Aplica um kernel gaussiano de raio escolhido como um filtro na imagem.
 |
|---|
| Figura 1: Filtro gaussiano. |
- Winvar filter: Filtro baseado na variância, calcula \(\left\lt x^2\right\gt-\left\lt x\right\gt^2\) dentro de um kernel de raio escolhido.
 |
|---|
| Figura 2: Filtro winvar. |
- Gabor filters: Calculados em direções \(\theta\) igualmente espaçadas, esses filtros são compostos de uma parte gaussiana e uma parte senoidal. Em 2D, a fórmula é:
 |
|---|
| Figura 3: Filtro Gabor em uma das direções \(\theta\). |
- Minkowsky functionals: Parâmetros morfológicos que descrevem a geometria dos dados, associados a volume, superfície, curvatura média e característica de Euler.
  |
|---|
| Figura 4: Filtros Minkowsky. |
- Variogram range: Mede a variação média dos valores em função da distância. O range é a distância onde a variação é máxima. É útil para diferenciar texturas e granulometrias.
 |
|---|
| Figura 5: Variogram range. |
Método Inferência Bayesiana
Este método utiliza a regra de Bayes para classificar os pixels da imagem, atualizando as probabilidades de um pixel pertencer a uma classe com base nas anotações.
A abordagem no GeoSlicer assume uma Distribuição Normal Multivariada para a função de verossimilhança, onde a média \(\mu_s\) e a matriz de covariância \(\Sigma_s\) de cada segmento são calculadas a partir das anotações:
Onde \(x_p\) é o vetor de pixels em uma janela, e \(\mu_s\) e \(\Sigma_s\) são a média e a covariância do segmento \(s\).
A inferência da probabilidade de cada segmento para um pixel é obtida pela regra de Bayes, e o segmento que maximiza essa probabilidade é escolhido.
Para otimizar o desempenho, são aplicados alguns tratamentos, como a transformação de percentil em imagens de MicroCT e a conversão para o formato HSV em imagens de lâminas delgadas. Além disso, para acelerar o processo, é possível calcular a covariância de forma esparsa, utilizando apenas os eixos ou planos principais, o que é especialmente útil em 3D.
Abaixo, alguns resultados da aplicação do método em imagens de tomografia e lâminas:
 |
|---|
| Figura 6: Segmentação semi-automática usando inferência Bayesiana em dados de MicroCT. |
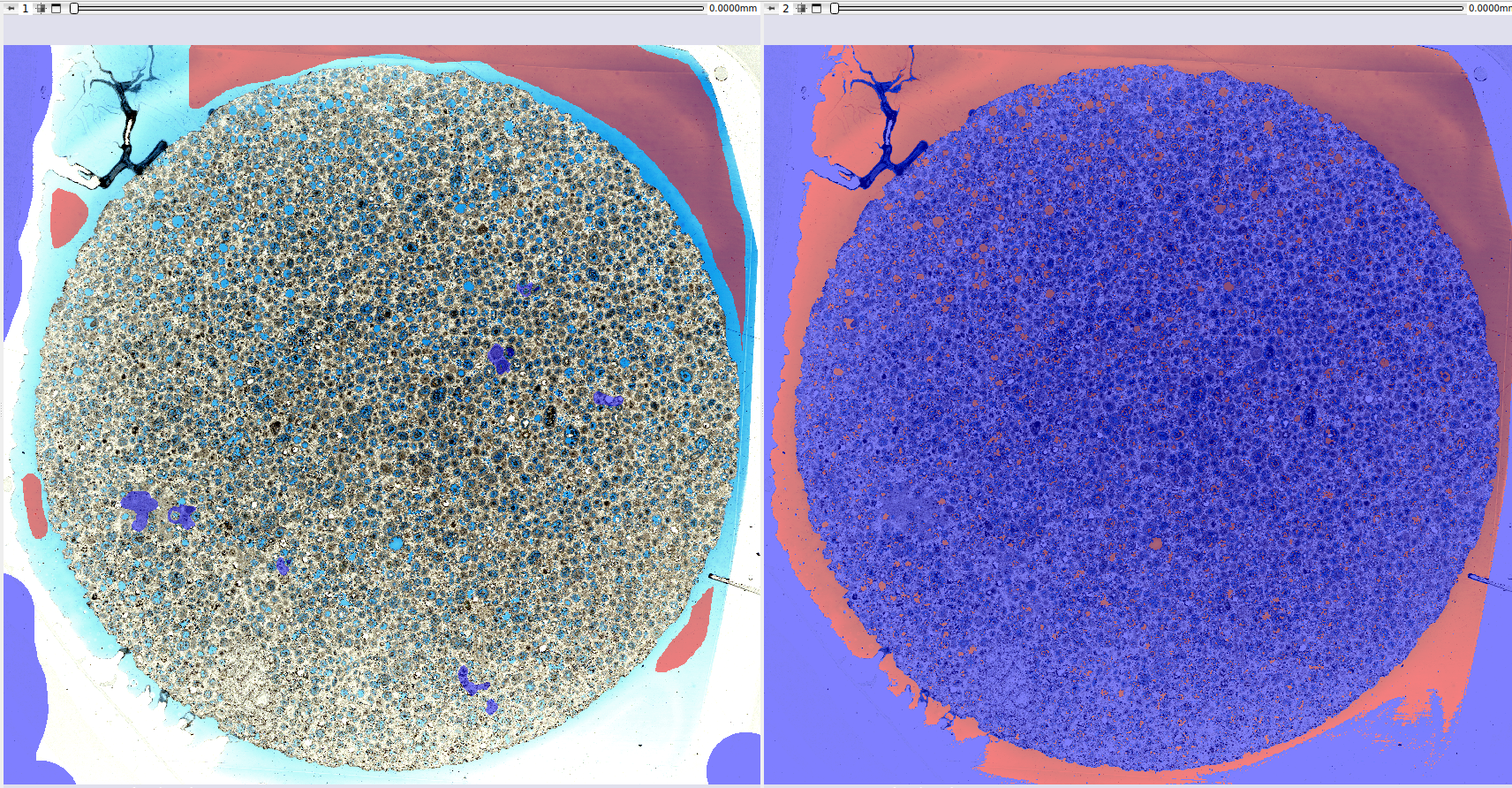 |
|---|
| Figura 7: Segmentação semi-automática usando inferência Bayesiana em dados de lâminas. |
Modelos Pré-treinados
O GeoSlicer oferece modelos pré-treinados baseados na arquitetura U-Net para resolver dois problemas comuns na microtomografia de rochas: a segmentação binária (poro/não-poro) e a segmentação basins (múltiplos minerais).
Treinamento
O treinamento dos modelos foi realizado com um vasto conjunto de dados (68 volumes para o modelo binário e 106 para o basins), aplicando uma transformação linear de histograma para facilitar a generalização. Os volumes foram recortados em subvolumes de 128³ voxels, e uma porção de 75% deles sofreu transformações aleatórias (aumento de dados) para melhorar a robustez do modelo. Para lidar com o desbalanceamento de classes (poros são menos comuns), foi utilizada a função de custo de Tversky, que ajusta a sensibilidade do modelo para classes minoritárias, melhorando a precisão na detecção de poros.
Resultados
Os modelos pré-treinados apresentam resultados de alta qualidade. O modelo de segmentação binária é especialmente preciso na identificação de poros, enquanto o modelo basins oferece uma segmentação completa dos diferentes minerais.
Segmentação Binária
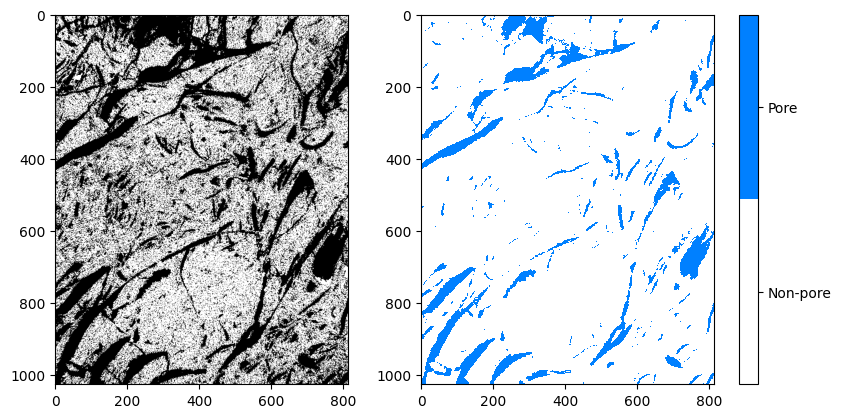 |
|---|
| Figura 8: Comparação entre a imagem original, a anotação e o resultado da segmentação binária. |
Segmentação Basins
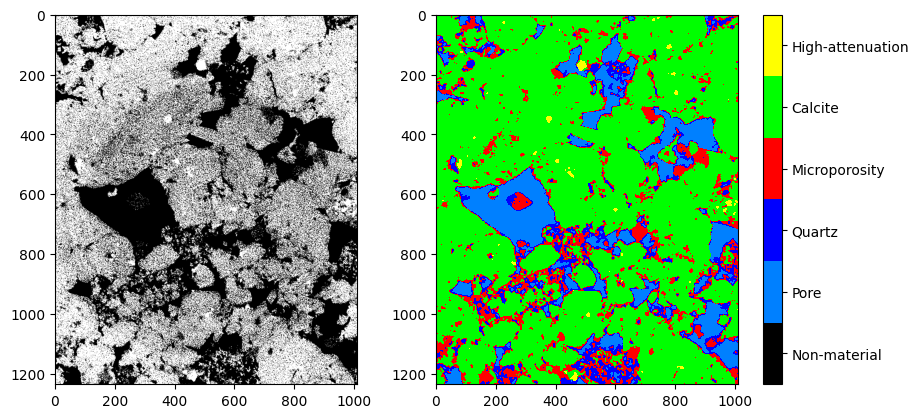 |
|---|
| Figura 9: Comparação entre a imagem original, a anotação e o resultado da segmentação basins. |
Referências
-
SCHMIDT, U. et al. (2018). Cell detection with star-convex polygons. In: Medical Image Computing and Computer Assisted Intervention–MICCAI 2018. Springer.
-
SALEHI, S. S. M. et al. (2017). Tversky loss function for image segmentation using 3D fully convolutional deep networks. In: Machine Learning in Medical Imaging. Springer.
-
WEIGERT, M. et al. (2020). Star-convex polyhedra for 3D object detection and segmentation in microscopy. In: Proceedings of the IEEE/CVF winter conference on applications of computer vision.
-
BAI, M. & URTASUN, R. (2017). Deep watershed transform for instance segmentation. In: Proceedings of the IEEE conference on computer vision and pattern recognition.
-
HE, K. et al. (2017). Mask r-cnn. In: Proceedings of the IEEE international conference on computer vision.
-
RONNEBERGER, O. et al. (2015). U-net: Convolutional networks for biomedical image segmentation. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015. Springer.