Pore Network

Simulation

This module can perform different types of simulations based on the results of the pore and connection table (created in the [Extraction] module). The simulations include: One-phase, Two-phase, Mercury injection, explained in the following sections.

All simulations have the same input arguments: The pore table generated from the network extraction and, when the volume is multiscale, the subscale model used and its parameterization.

Figure 1: Input of the pore table generated with the Extraction module.

One-phase

The one-phase simulation is mainly used to determine the absolute permeability (\(K_{abs}\)) property of the sample.

Figure 2: Single-phase simulation.

Three different solvers can be used for this type of simulation:

• pypardiso (recommended): yields the best results, converging even in situations with very discrepant radii;
• pyflowsolver: includes an option to select the stopping criterion, but with lower performance than pypardiso;
• openpnm: the most traditionally used option;

Figure 3: Pyflowsolver option and stopping criterion. The other options (pypardiso and openpnm) do not have this criterion.

When the conductivity values are very different for the same sample, and this sample percolates more through the subscale, we may have problems converging to the solution. Because of this, we added an option to limit the values at high conductivities.

Figure 4: Options for limiting conductivity values.

In addition, single-phase simulation can be performed in a single direction or in multiple directions using the Orientation scheme parameter.

Figure 5: Orientation scheme used.

Two-phase

The two-phase simulation consists of initially injecting oil into the sample and increasing its pressure so that it invades virtually all pores, in a process known as drainage. After this first stage, the oil is replaced with water and the pressure is increased again to allow the water to invade some of the pores that were previously filled with oil, expelling the latter. This second process is known as imbibition. By measuring the permeability of the rock in relation to absolute permeability, as a function of water saturation during this process, we obtain the curve known as the relative permeability curve (\(K_{rel}\)).

Since each rock can interact physically or chemically with oil and water in different ways, we need a fairly large variety of parameters to calibrate the results in order to model and simplify this interaction, so that we can extract some physical meaning from the rock properties from the simulation. Below, we list some parameters that can be found in the two-phase simulation available in GeoSlicer.

Currently, we have two algorithms available in GeoSlicer to perform two-phase simulation. The first is PNFlow, which is a standard algorithm implemented in C++, and the second is an algorithm developed by LTrace in Python.

Save/Load parameter selection table

To facilitate the reproduction of simulations that run on the same set of parameters, the interface has options to save/load parameters from tables that are saved with the project. Thus, when calibrating the set of parameters, the user can save this information for later analysis or use these same parameters in another sample.

Fluid properties

In this section, you can change the parameters of the fluids (water and oil) used in the simulation:

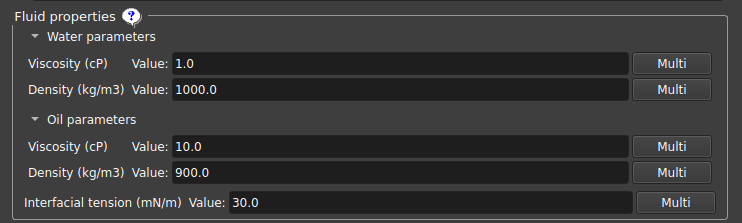Figure 7: Input of fluid parameters (water and oil).

Contact angle options

One of the main properties that affect the interaction of a liquid with a solid is wettability, which can be determined from the contact angle formed by the former when in contact with the latter. Thus, if the contact angle is close to zero, there is a strong interaction that “binds” the liquid to the solid, whereas when the contact angle is close to 180°, the interaction of the liquid with the surface is weak and it can flow more easily through it.

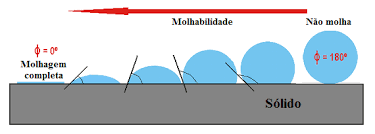Figure 8: Visual representation of the concept of wettability and contact angle.

We modeled the contact angles from two distributions used at different times: the Initial contact angle, which controls the contact angle of the pores before oil invasion; and the Equilibrium contact angle, which controls the contact angle after oil invasion. In addition to the base distributions used in each case, there is an option to add a second distribution for each of them, so that each pore is linked to one of the two distributions, with the “Fraction” parameter being used to determine what percentage of pores will follow the second distribution in relation to the first.

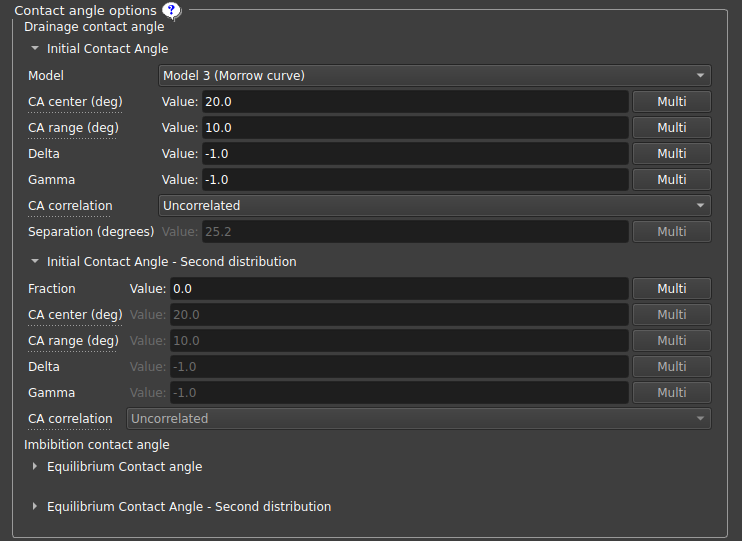Figure 9: Contact angle distribution parameters.

Each angle distribution, whether primary or secondary, initial or equilibrium, has a series of parameters that describe it:

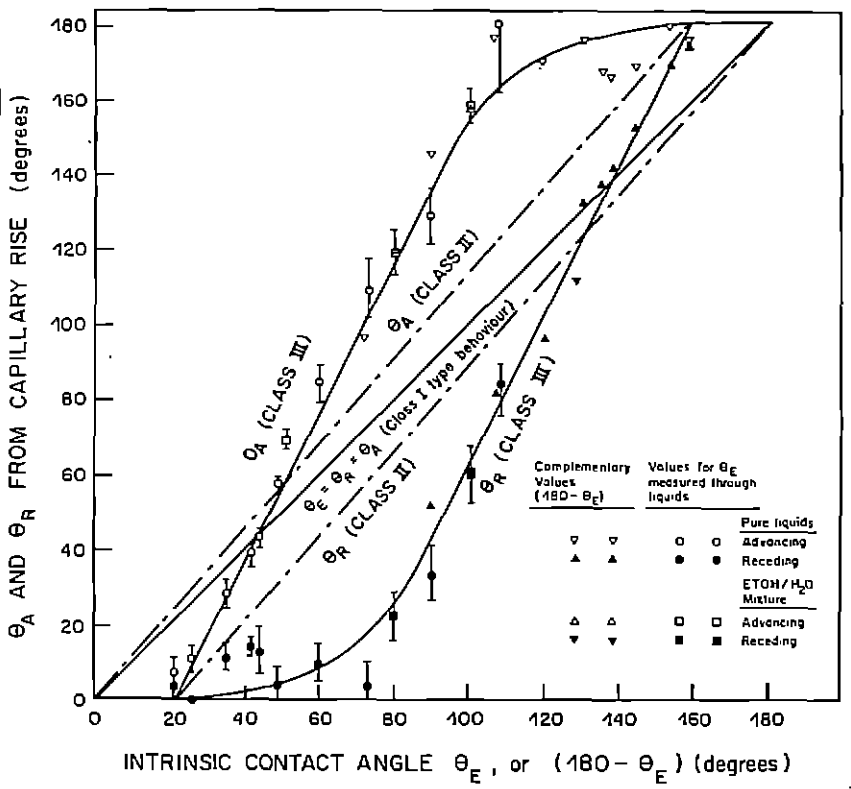
• Model: allows modeling the hysteresis curves between advance/retreat angles from the intrinsic angles:

  • Equal angles: advance/retreat angles identical to the intrinsic angle;
  • Constant difference: constant difference between the advance/retreat angles and the intrinsic angle;
  • Morrow curve: advance/retreat curves determined by Morrow curves;

Figure 10: Curves for each of the contact angle models implemented in GeoSlicer. Image taken from N. R. Morrow, 1975 (https://doi.org/10.2118/75-04-04).

• Contact angle distribution center: Defines the center of the contact angle distribution;
• Contact angle distribution range: Distribution range (center-range/2, center+range/2), with the minimum/maximum angle being 0º/180º, respectively;
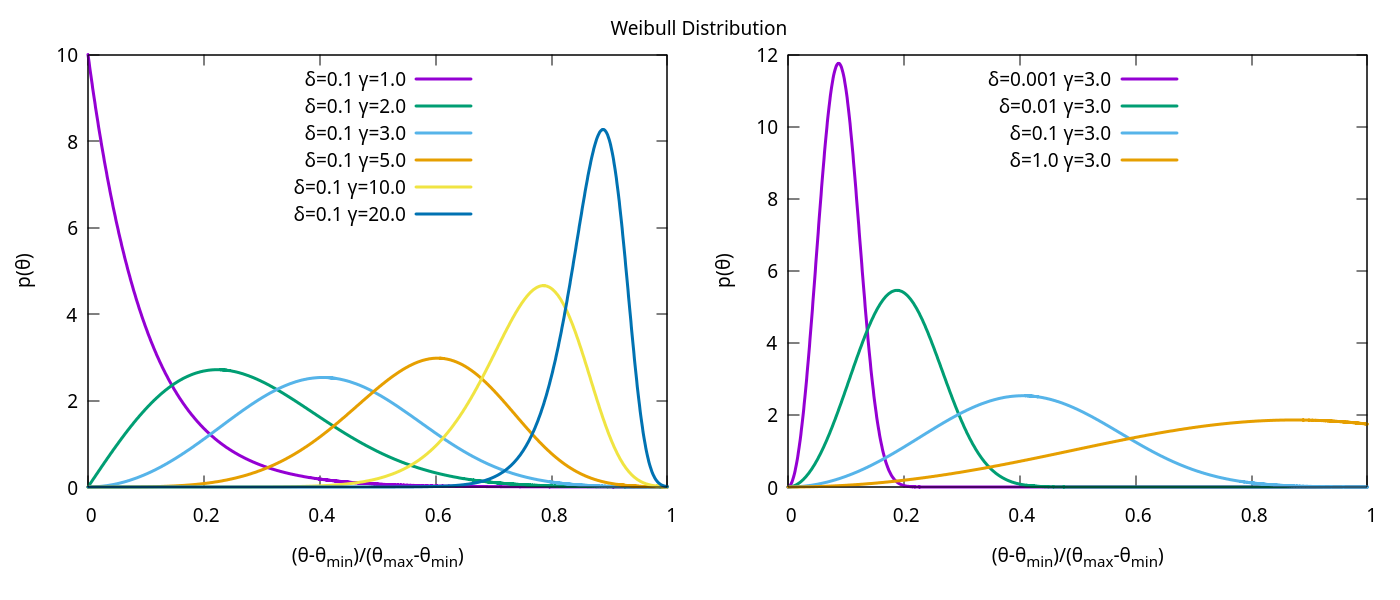
• Delta, Gamma: Truncated Weibull distribution parameters; if a negative number is chosen, a uniform distribution is used; If positive numbers are chosen, it uses the following probability distribution: \(p(\tilde\theta)=\frac{\gamma}{\delta}\frac{\tilde\theta^{\gamma-1}e^{-\tilde\theta^\gamma/\delta}}{1-e^{-1/\delta}}\) where \(\tilde\theta\in[\theta_{min},\theta_{max}]\). Some ideas for parameters for this distribution are graphed below:

Figure 11: Weibull distribution.

• Contact angle correlation: Chooses how the contact angle will be correlated to the pore radius: Positive radius defines larger contact angles for larger radii; Negative radius does the opposite, assigning larger angles to smaller radii; Uncorrelated means independence between contact angles and pore radius;
• Separation: If the chosen model is constant difference, defines the separation between advance and retreat angles;

Other parameters are defined only for the second distribution:

• Fraction: A value between 0 and 1 that controls which fraction of the pores will use the second distribution instead of the first;
• Fraction distribution: Defines whether the fraction will be determined by the number of pores or total volume;
• Correlation diameter: If Fraction correlation is chosen as Spatially correlated, defines the most likely distance to find pores with the same contact angle distribution;
• Fraction correlation: Defines how the fraction for the second distribution will be correlated, if spatially correlated, for larger pores, smaller pores, or random;

Execution Mode

The user can choose between two execution modes for running the two-phase simulation:

• Local: Runs the simulation directly on the user’s machine.
  In this mode, the user can define the Max subprocesses simulation option, which controls how many single-threaded subprocesses will run in parallel. The recommended value is about two-thirds of the total available CPU cores for optimal performance without overloading the system.

• Remote: Sends the simulation to be executed on a configured computing cluster.
  In this mode, the user specifies the Number of jobs into which the simulation will be divided. Ideal for very large sensitivity tests. The interface on the right will show the progress of the simulation, and the user can also Open the partial results for inspection before completion.

Figure 12a: Execution mode selection for the two-phase simulation.

Figure 12b: Job options.

This flexibility allows the user to take advantage of local processing for smaller test runs or to leverage cluster computing resources for more complex or large-scale simulations.

Simulation options

This section of parameters is dedicated to controlling the parameters related to the simulation itself.

Figure 13: Simulation parameters.

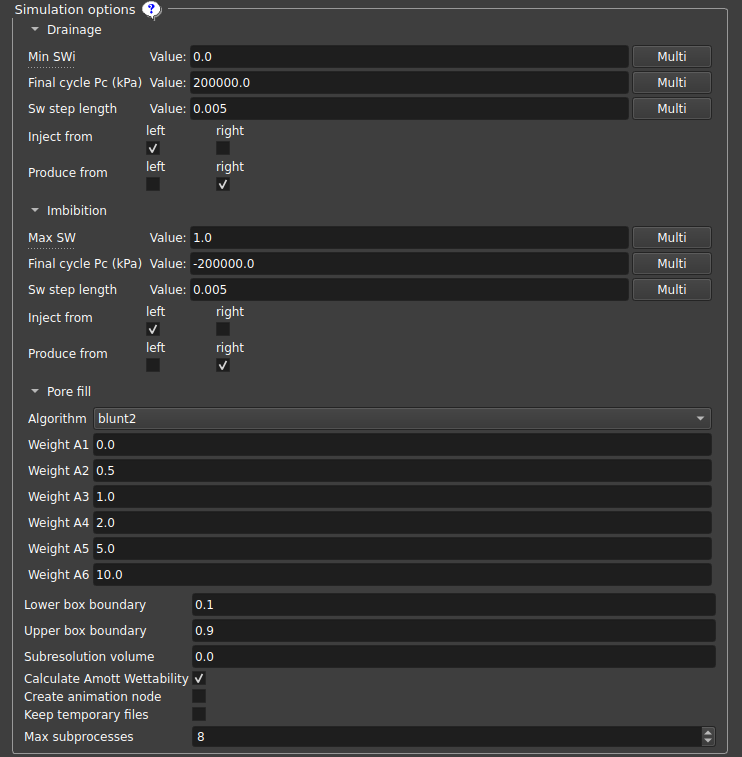
• Minimum SWi: Sets the minimum SWi value, interrupting the drainage cycle when the Sw value is reached (SWi may be higher if water becomes trapped);
• Final cycle Pc: Interrupts the cycle when this capillary pressure is reached;
• Sw step length: Sw step used before checking the new permeability value;
• Inject/Produce from: Defines on which sides the fluid will be injected/produced along the z-axis; the same side can both inject and produce;
• Pore fill: Determines which mechanism dominates each individual pore filling event;
• Lower/Upper box boundary: Pores with a relative distance on the Z axis from the edge to this plane value are considered “left”/“right” pores, respectively;
• Subresolution volume: Considers that the volume contains this fraction of subresolution porous space that is always filled with water;
• Plot first injection cycle: If selected, the first cycle, oil injection into a fully water-saturated medium, will be included in the output graph. The simulation will run regardless of whether the option is selected or not;
• Create animation node: Creates an animation node that can be used in the “Cycles Visualization” tab;
• Keep temporary files: Keeps the .vtu files in the GeoSlicer temporary files folder, one file for each stage of the simulation;
• Max subprocesses: Maximum number of single-thread subprocesses to be executed; The recommended value for an idle machine is two-thirds of the total number of cores;
• Number of jobs: number jobs of into which the simulation will be divided on the cluster;

Since we have a vast number of parameters that can be modified to model the experiment from the simulation, it becomes useful to vary these parameters more systematically for an in-depth analysis of their influence on the results obtained.

To do this, the user can select the “Multi” button available in most parameters. When clicking on Multi, three boxes appear with start, end, and step options, which can be used to run several simulations in a linearly distributed table of the values of these parameters. If more than one parameter is chosen with multiple values, simulations run with all possible parameter combinations, which can considerably increase the number of simulations and the time to execute them.

Upon completion of the simulation set, the user can perform analyses to understand the relationships between the simulation results and the parameters selected in the Krel EDA tab.

Mercury injection

In addition to the one- and two-phase simulations, this module also offers a simulation of the Mercury intrusion experiment.

Figure 14: Mercury intrusion simulation.

Mercury intrusion is an experiment in which liquid mercury is injected into a reservoir rock sample under vacuum, with increasing pressure. The volume of mercury invading the sample is measured as a function of mercury pressure. Since the contact angle of liquid mercury with mercury vapor is approximately independent of the substrate, analytical models, such as the tube bundle model, can be used to calculate the pore size distribution of the sample.

The mercury intrusion test is relatively affordable, and its main relevance in the context of PNM lies in the ability to perform the simulation on a sample for which experimental results of Mercury Intrusion Capillary Pressure (MICP) curves are available. This allows the comparison of results to validate and calibrate the pore network extracted from the sample, which will be used in one- and two-phase simulations.

To facilitate the analysis of sub-resolution pore radius assignment, the code in GeoSlicer will produce, in addition to the graphs obtained by the simulation in OpenPNM, graphs of pore and throat radius distributions and also volume distributions, separating them into resolved pores (which are not altered by subscale assignment) and unresolved pores. This allows the user to check whether the subscale model has been applied correctly.

Subscale Model

In the case of a multiscale network, since the subscale radii cannot be determined from the image itself because they are outside the resolution, it is necessary to define a model for assigning these radii. Some options currently available are:

• Fixed radius: All subresolution radii are the same size as chosen in the interface.

• Leverett Function - Sample Permeability: Assigns an inlet pressure based on the J Leverett curve based on the permeability of the sample;

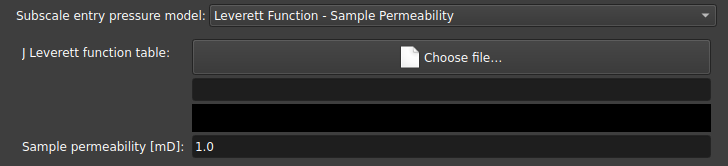
• Leverett Function - Permeability curve: Also uses the J Leverett curve but with a curve defined for permeability instead of a value;

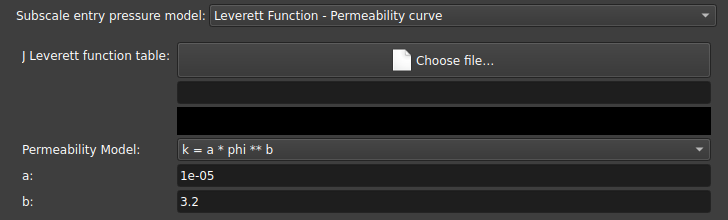
• Pressure Curve and Throat Radius Curve: Assigns subresolution radii based on the curve obtained from a mercury injection experiment. The inlet pressure data can be used by volume fraction, or the equivalent radius can be used as a function of volume fraction;

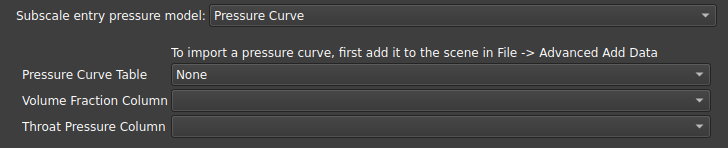
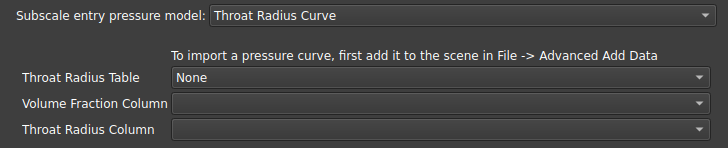
The chosen subscale model has no impact on uniescalar network simulations, since all radii are already determined.

---

Extractor

This module is used to extract the pore and bond network from: an individualized segmentation of pores (Label Map Volume) performed by a watershed algorithm, generating a uniscalar network; or from a porosity map (Scalar Volume), which will generate a multiscalar model with resolved and unresolved pores.

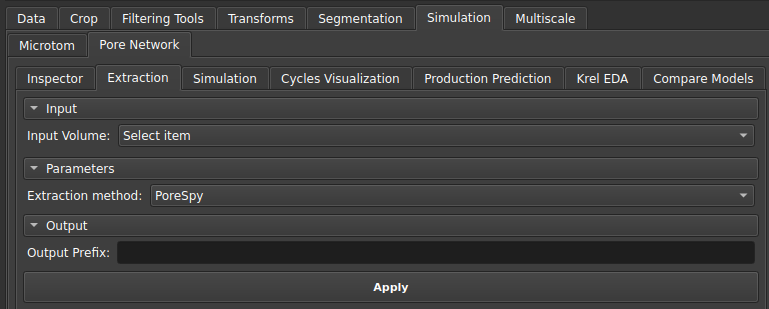Figure 1: Extraction Module Interface.

After extraction, the following will be available in the GeoSlicer interface: the pore and throat tables, as well as the network visualization models. The generated tables will be the data used in the subsequent simulation step.

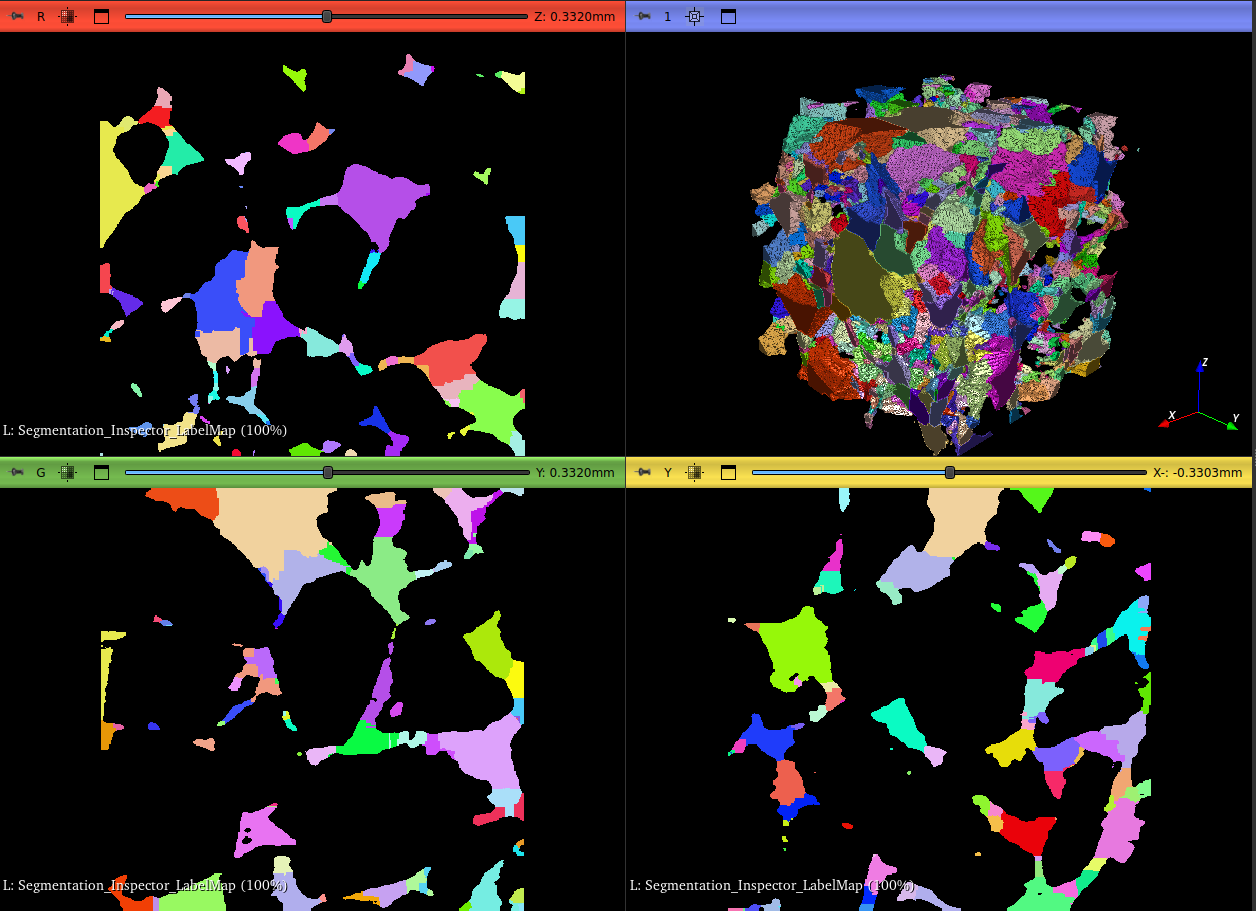Figure 1: On the left, the Label Map used as input for extraction, and on the right, the extracted uniscalar network.

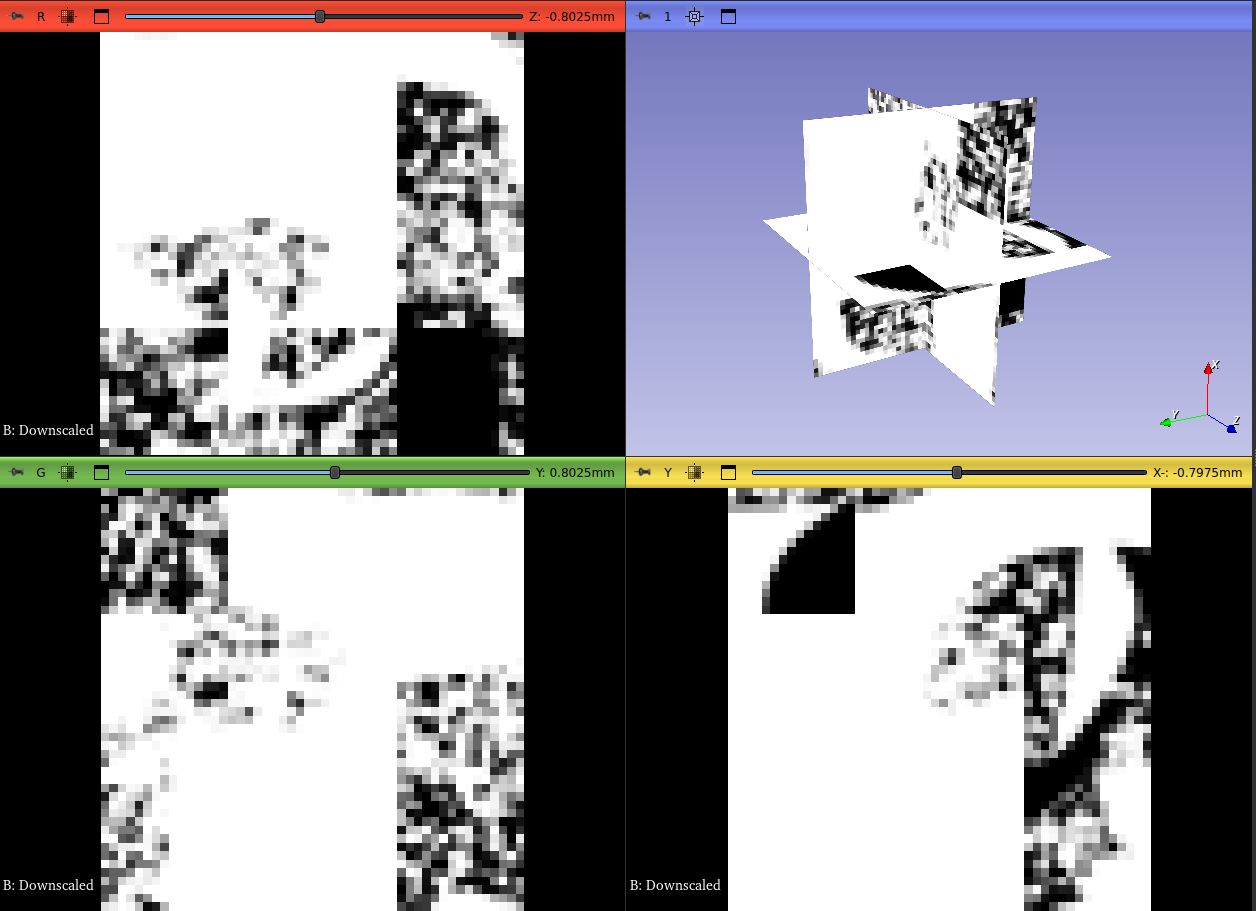Figure 2: On the left, the Scalar Volume used as input for extraction, and on the right, the extracted multiscalar network, where blue represents resolved pores, and pink represents unresolved pores.

Color Scale:

Spheres (Pores):

• Blue - Resolved pore
• Magenta - Unresolved pore

Cylinders (Throats):

• Green - Throat between resolved pores
• Yellow - Throat between a resolved and an unresolved pore
• Red - Throat between unresolved pores